dx = 
+ C
3.1 Primitivní funkce, neurčitý integrál
Teorii naleznete v kapitole 6.1 Multimediální encyklopedienebo v kapitole 3.1 Breviáře
Příklad 1
Pro x∈(-1,1) ověřte podle definice primitivní funkce platnost rovnosti dx = + C
Řešení
Podle definice neurčitého integrálu (primitivní funkce) platí:
[∫f(x)dx]
= f(x)dx
Vyjádřeno slovně, zderivujeme-li primitivní funkci 
(někdy značíme primitivní funkci také F(x)), obdržíme funkci f(x).
Ve skutečnosti je tedy tento příklad cvičením na derivování.
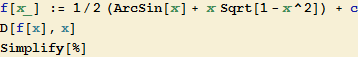
Příklad 2
Pro x≠(2k+1) 
ověřte pomocí definice primitivní funkce platnost rovnosti ∫ tg x dx = -ln |cos x| + C.
Podle definice primitivní funkce, zderivuji-li funkci -ln |cos x| + C, musím obdržet funkci tg x, ke které byla původní funkce primitivní.
Řešení
Příklad 3
Vypočítejte následující neurčitý integrál: 
.
Řešení
Jedná se o výpočet primitivní funkce k funkci f(x) = 
. Výpočet primitivní funkce se také nazývá integrace. Chceme-li umět integrovat funkce, musíme znát celou řadu vzorců integrálů elementárních funkcí, dále větu o linearitě integrálu, větu "per partes", věty o substituci a i tak integrování složitějších funkcí vyžaduje jistou zkušenost a znalost určitých "triků" v algebraických úpravách funkcí tak, abychom je převedli do tvaru, který lze snadno integrovat.
V Mathematice se integrace provádí následovně:
Ověřit správnost výsledku můžeme snadno, zderivujeme-li výslednou funkci, měli bychom opět obdržet funkci původní, ke které jsme primitivní funkci hledali.
Příklad 4
Vypočítejte následující neurčitý integrál:
dx
Řešení
